While reaching to conclusion about a large volume of data, we prefer to take samples from the whole population and then we analyze them and reach to a conclusion. We expect that the samples taken represents the whole population sufficiently or at least reasonably.
We want to use our judgment as less as possible as the judgment sometimes can lead towards biasness. As the Simple Random Sampling involves more judgment and Stratified Random Sampling needs complex process of classification of the data into different classes, we use Systematic Random Sampling.
We can also say that this method is the hybrid of two other methods (viz. Simple Random Sampling and Stratified Random Sampling).
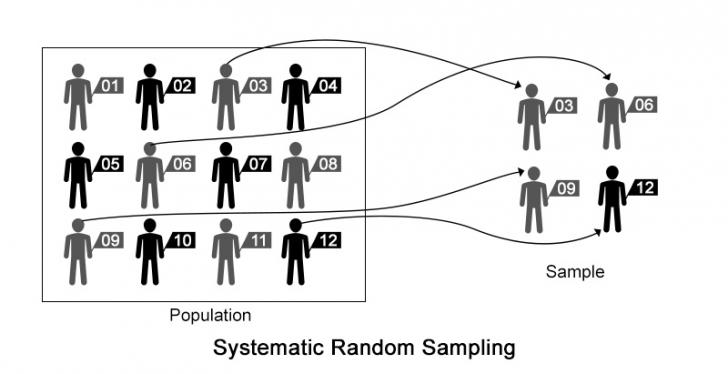
The figure above shows us how we conduct the process of choosing the samples from the given population. The first sample is chosen at random and then the remaining are chosen by leaving two items after the previous sample.
Process of Systematic Random Sampling
- Determine th size of the population.
- Determine the sample size (number of samples to be taken).
- Calculate the number of items in the population to be represented by each sample.
No of items in the population to be represented by each sample (n) = Population Size $div$ Sample Size. - Select any item as the first sample and choose next samples which comes at nth position after the previous one.
- Collect the samples and draw an appropriate conclusion.
Advantages:
- easier than Stratified Random Sampling and more effective than Simple Random Sampling
You do not need to classify data in Systematic Random Sampling as in Stratified Random Sampling. And it is more effective than Simple Random Sampling as it avoids judgment. - Cost Effective
Stratification would cost lots of resources. Thus Systematic Random Sampling is more effective than others. - Avoids Judgments
It involves probability to a greater extent. So, judgments are avoided. Once the first sample is chosen, the role of the judgment finishes. - Less Time Consuming
It does not cost the time for stratification nor it leaves any doubt on reliability. - Higher degree of Control
We can control the sample size, first sample and other means of control to complete the process. Thus the level of control is always higher.
Disadvantages:
- Size of the population may not be known before the sampling starts
Suppose that we want to survey on the brand of cigarette that the smokers want. We may not know how many of the population smoke or all the brands of the cigarettes available in the market. - Assumption that the population is uniform may not always prove to be true
We can not say that the population is enough uniform. Sometimes it can also be true that the exceptional items appear on the portion of population that are taken as samples. This makes the system defunct.