There are many technical terminologies that we need to understand to improve our learning of set theory. Some of them are explained below:
- Sets
- Universal Set
- Venn Diagrams
- Intersection of Sets
- Union of Sets
- Disjoint Sets
- Difference of Sets
- Sub Sets
- Complement of a Set
- Number of Subsets from a set
1. Sets
Sets are the the collection of different objects having at least one or more properties common amongst them.
Sets can comprise no any elements, a few elements or infinite number of elements. Examples of set are Set of Planets of Solar System, Set of Continents, Set of Constellations etc.
Concept of sets can be very much useful to understand analyze and interpret the different relationships between multiple groups of data/ information.
Examples of sets:
a. Set of the mountains of Nepal with height 8000 m or above.
{ Everest, Kangchenjunga, Lhotse, Makalu, Cho Oyu, Dhaulagiri, Manaslu, Annapurna }
b. Set of Natural Numbers below 8
{ 1, 2, 3, 4, 5, 6, 7}
c. Set of US presidents of 21st century:
{ Bill Clinton, George W. Bush, Barack Obama }
d. Set of German Chancellors Since 1980:
{ Helmut Schmidt, Helmut Kohl, Gerhard Schröder, Angela Merkel }
e. Set of SAARC nations:
{Nepal, Sri-Lanka, India, Bhutan, Afghanistan, Pakistan, Maldives, Bangladesh}
f. Set of Colors in Rainbow:
{ Red, Orange, Yellow, Green, Blue, Indigo, Violet}
2. Universal Set
Universal set is the set comprising of all the elements that are in consideration for a specific case. Some of the corresponding Universal sets for above discussion would be:
| Set | Universal Set |
|---|---|
| Mountains of Nepal | Mountains |
| Numbers below 100 | Whole Numbers |
| Presidents of USA since 1900 | Presidents of USA till date |
| German Chancellors since 1900 | German Chancellors till date |
| Countries in Asia | Countries of the world |
| Colors present in the body of Peacock | Primary and Secondary Colors |
3. Venn Diagrams
Venn Diagrams are a way to visually represent sets and their relationships.
In Venn Diagrams, the Universal set is represented by a rectangle and the other sets are represented by circles or ovals, the elements are kept inside these circles in such a way as to accurately describe their membership.
Venn Diagrams for some of the sets discussed above are:
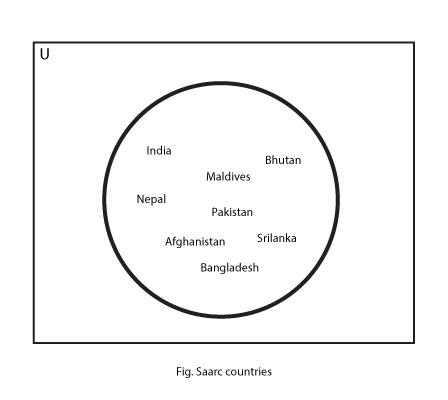
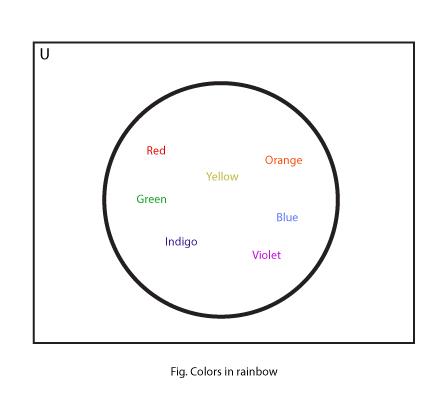
4. Intersection of Sets
The set formed by way of taking only the elements which are present in each and every one of those sets in consideration is known as the intersection of the sets.
Consider a Universal Set
U = { Natural Numbers below 20} with following sets:
A = { Natural Numbers below 10}
B = { Even Numbers below 20}
Then, the Venn Diagram for the Intersection of A and B (i.e. A $bigcap$ B) would be:
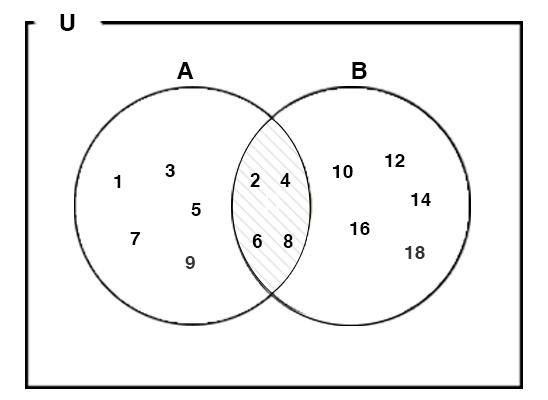
5. Union of Sets
Union of Sets is a set of the elements which are present in at least one of the sets in consideration . The symbol for Union is represented by U. In other words,
The set comprising up of every member one of, some of or all of the sets in consideration is known as Union of Sets.
Union of some specific sets has all of the members/elements that any of its member sets has.
Then, the Venn Diagram for the Union of sets A and B (i.e. A $bigcup$ B) would be:
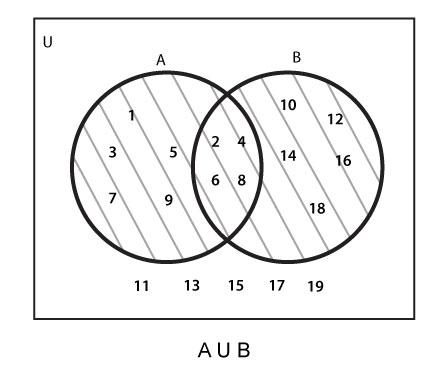
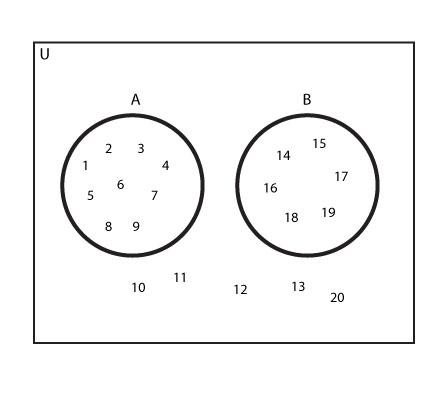
6. Disjoint Sets
Two sets are said to be disjoint if they have no any elements in common.
Consider a Universal Set
U = { Natural Numbers below 20} with following sets:
A = { Natural Numbers below 10}
B = { Natural Numbers above 13 and below 20}
Then, the Venn Diagram for them would be:
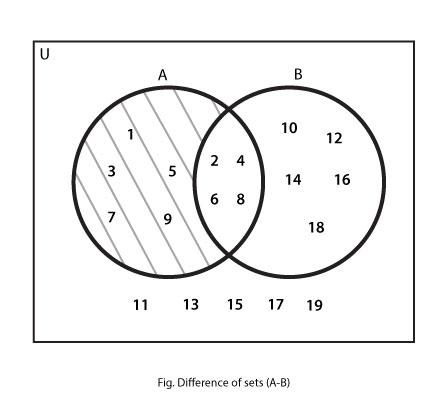
7. Difference of Sets
The group of elements of a set that excludes another elements of another set is known as Difference of the two sets.
If we have two sets A and B, the group of elements of A which are not an elements of B is called A-B (To be read as ‘A minus B’ or ‘A Difference B’)
Eg:
Consider a Universal Set
U = { Natural Numbers below 20} with following sets:
A = { Natural Numbers below 10}
E = { Even Numbers below 20}
Then, the Venn Diagram for the Difference of A and B (i.e A – B) would be:
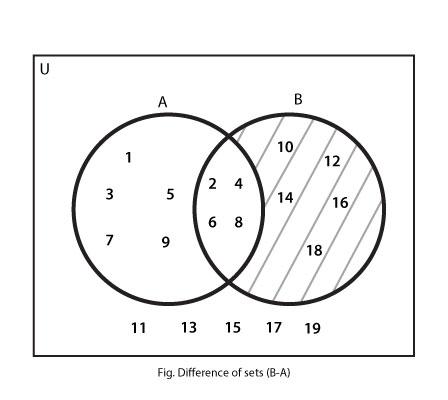
Similarly, The Venn Diagram for (B – A) becomes:
8. Sub Sets
A set formed by taking the some or all of the elements from another set is known as sub- set.
If A= { Multiples of 4 which are less than 20} and B = { Multiples of 2 which are smaller than 20}
Then,
A ={ 4, 8, 12, 16}
B = { 2, 4, 6, 8, 10, 12, 14, 16, 18}
$Rightarrow$ A $subset$ B
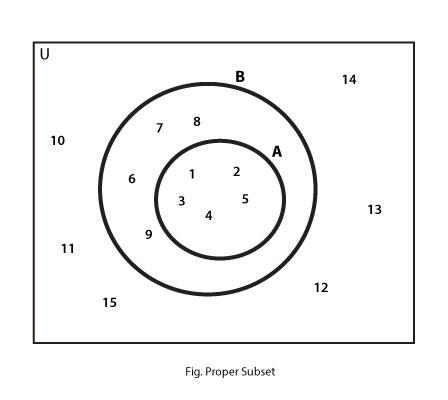
Proper Subset
If the subset does not contain all the elements of another set then the first set is said to be the proper subset of the second set.
eg:
Consider a Universal Set
U = { Natural Numbers below 20} with following sets:
B = { Natural Numbers below 10} and,
A = { Natural numbers below 5}
Here, since all the elements in A are also present in B, A is the subset of B. But since not all elements of B are present in A, A is further called a proper subset of B.
A $subset$ B
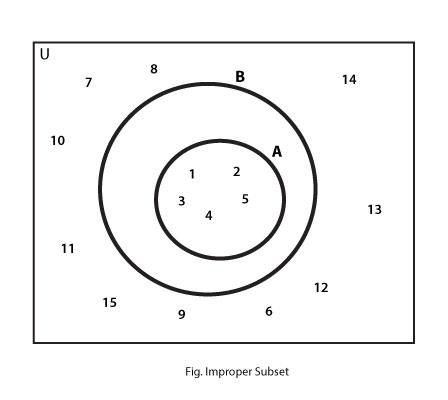
Improper Subset
If the subset contains all the elements of another set then the first set is said to be the improper subset of the second set.
U = { Natural Numbers below 20 } with following sets:
A = { Natural Numbers below 5 } and,
B = { Natural numbers below 10 }
In this case, since all the elements of B are also contained in A, A is the Improper Subset of B
M $subseteq$ N
The Venn Diagram would be:
9. Complement of a Set
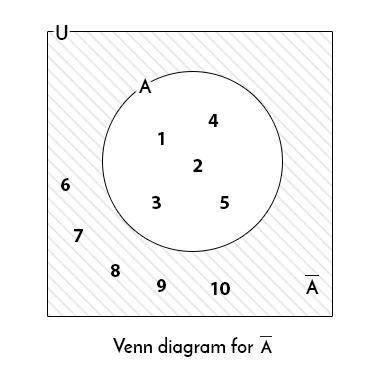
The collection of all the elements in the Universal set except those that are members of a set/ region in consideration is called Compliment of a set/region.
Consider a Universal Set
U = { Natural Numbers till 10 } and
set A = { Natural Numbers till 5 }
Then, the Venn Diagram for (A)c is:
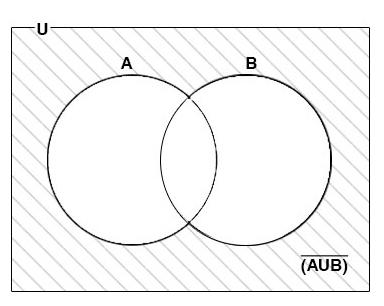
We can calculate the complement of a region. The following Venn Diagram for the complement of (A $bigcup$ B).
10. Number of Subsets from a set
The number of subsets that can be formed from a set with specific number of elements is given as:
Number of subsets = 2n
Where, n= number of elements in that set
For example,
A= {a, b} n= 2
Thus, number of Subsets that can be formed: 4
The subsets of A are:
{a}, {b}, {a, b,}, {$Phi$}