Parallelogram Law of Vector Addition

Statement of Parallelogram Law

If two vectors acting simultaneously at a point can be represented both in magnitude and direction by the adjacent sides of a parallelogram drawn from a point, then the resultant vector is represented both in magnitude and direction by the diagonal of the parallelogram passing through that point.

Derivation of the law

Note: All the letters in bold represent vectors and normal letters represent magnitude only.

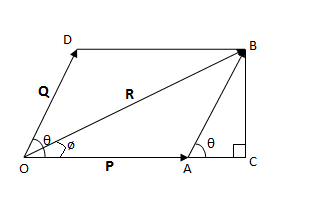
Let P and Q be two vectors acting simultaneously at a point and represented both in magnitude and direction by two adjacent sides OA and OD of a parallelogram OABD as shown in figure.

Let θ be the angle between P and Q and R be the resultant vector. Then, according to parallelogram law of vector addition, diagonal OB represents the resultant of P and Q.

So, we have

R = P + Q

Now, expand A to C and draw BC perpendicular to OC.

From triangle OCB,

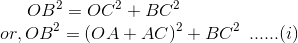
In triangle ABC,

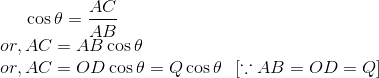
Also,

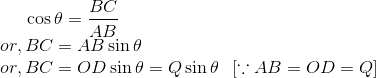
Magnitude of resultant:

Substituting value of AC and BC in (i), we get

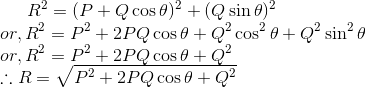
which is the magnitude of resultant.

Direction of resultant: Let ø be the angle made by resultant R with P. Then,

From triangle OBC,

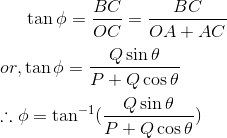
which is the direction of resultant.

Numerical Problem

Two forces of magnitude 6N and 10N are inclined at an angle of 60° with each other. Calculate the magnitude of resultant and the angle made by resultant with 6N force.

Solution:

Let P and Q be two forces wih magnitude 6N and 10N respectively and θ be angle between them. Let R be the resultant force.

So, P = 6N, Q = 10N and θ = 60°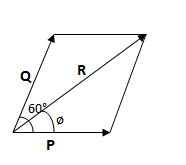

We have,

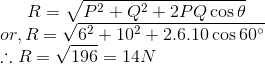
which is the required magnitude

Let ø be the angle between P and R. Then,

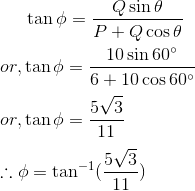
which is the required angle.