Triangle Law of Vector Addition

Statement of Triangle Law

If 2 vectors acting simultaneously on a body are represented both in magnitude and direction by 2 sides of a triangle taken in an order then the resultant(both magnitude and direction) of these vectors is given by 3^rd side of that triangle taken in opposite order.

Derivation of the law

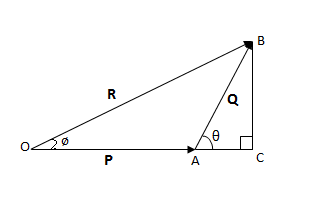
Consider two vectors P and Q acting on a body and represented both in magnitude and direction by sides OA and AB respectively of a triangle OAB. Let θ be the angle between P and Q. Let R be the resultant of vectors P and Q. Then, according to triangle law of vector addition, side OB represents the resultant of P and Q.

So, we have

R = P + Q

Now, expand A to C and draw BC perpendicular to OC.

From triangle OCB,

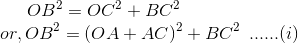
In triangle ACB,

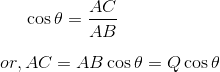
Also,

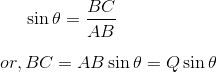
Magnitude of resultant:

Substituting value of AC and BC in (i), we get

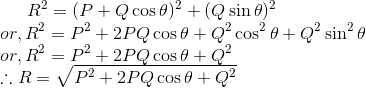
which is the magnitude of resultant.

Direction of resultant: Let ø be the angle made by resultant R with P. Then,

From triangle OBC,

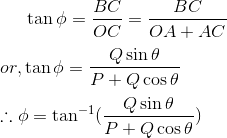
which is the direction of resultant.