When we select a limited number of elements from large group of elements (population) for sampling, we want to make sure that the samples taken correctly represent the population. How much our analysis of the limited dataset agrees with the characteristics of the population depends largely on the method of sampling used.
One way of selecting samples from the population is by dividing the whole population into small strata consisting up of elements with some similar characteristics and then choosing such number of samples from each of them so as to proportional to the size of the stratum.
This method of sampling is called Stratified Random Sampling and it is a kind of Probability Sampling.
Process of Stratified Random Sampling
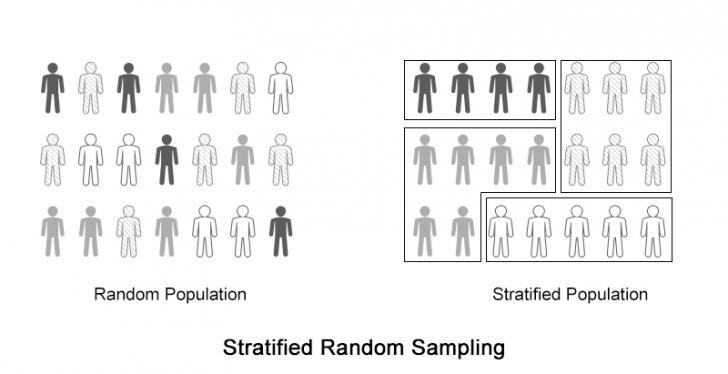
The above figure shows how different types of items are distributed in a random population. We need to stratify the population.
After the population is stratified as above, we can move on to the calculation and analysis.
Calculation
Imagine, for instance, you are appointed as the Head of the Investigation Team for a suspected fraud in a company in a fiscal year, you have been provided with 100,000 journal entries that were entered during the period of suspicion. You will not be examining all of the transactions as you will not be provided years and years for the single investigation.
If you choose to use stratified random sampling, you proceed as follows:
- Categorize all the journal entries into different classes of entries (Strata) eg:
- Sales Vouchers = 70,000
- Purchase Invoices =12,000
- Salary Invoices =7,500
- Purchase of Fixed Assets = 500
- Others = 10,000
- Decide for the size of the sample (Assume 2000 in this case)
- Calculate the number of samples to be taken from each of the Stratum. eg:
Number of items to be represented by a single sample
= Total Number of Elements in the Population $div$ The number of Samples to be taken
= 100,000 $div$ 2,000
= 50
Now, the numbers of samples to be taken from each of the stratum
- Sales Vouchers
= Number of items in the strata $div$ 50
= 70,000 $div$ 50
= 1,400 - Purchase Invoices
= Number of items in the strata $div$ 50
= 12,000 $div$ 50
= 240 - Salary Invoices
= Number of items in the strata $div$ 50
= 7,500 $div$ 50
= 150 - Purchase of Fixed Assets
= Number of items in the strata $div$ 50
= 500 $div$ 50
= 10 - Others
= Number of items in the strata $div$ 50
= 10,000 $div$ 50
= 200
Now, you can examine the number of items as stated above and reach your conclusion.
Advantages:
- Stratified Random Sampling provides better precision as it takes the samples proportional to the random population.
- Stratified Random Sampling helps minimizing the biasness in selecting the samples.
- Stratified Random Sampling ensures that no any section of the population are underrepresented or overrepresented.
- As this method provides greater precision, greater level of accuracy can be achieved even by using small size of samples. This saves resources.
Disadvantages:
- Stratified Random Sampling requires more administrative works as compared with Simple Random Sampling.
- It is sometimes hard to classify each kind of population into clearly distinguished classes.
- Stratified Random Sampling can be tedious and time consuming job to those who are not keen towards handling such data.