For two sets A and B, the union of A and B (denoted by A∪B) is the set of all distinct elements that belong to set A or set B. In mathematical form,
A∪B = { x: x∈A or x∈B}
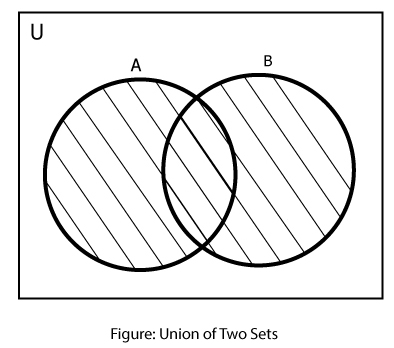
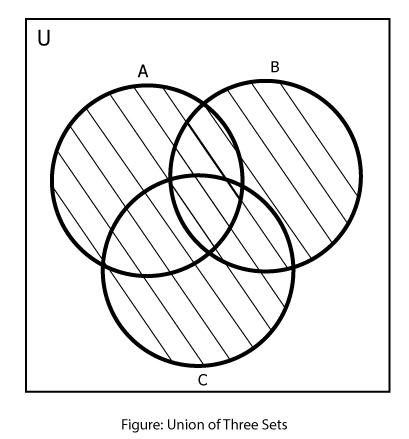
Similarly, for three sets A, B and C,
A∪B∪C = { x: x∈A or x∈B or x∈C}
Examples of Union of Sets
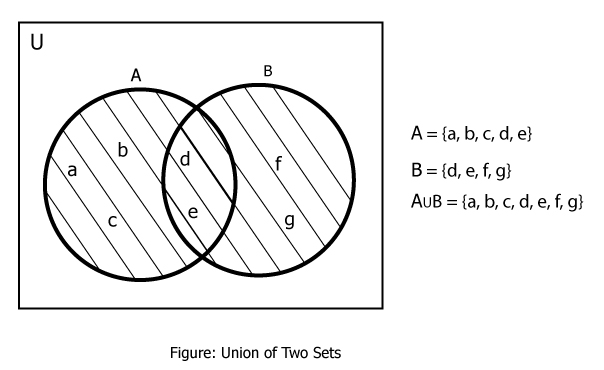
Example #1: Union of Two Sets With Venn Diagram
If A = {a, b, c, d, e} and B = {d, e, f, g}, find A∪B.
Here,
A∪B = {a, b, c, d, e} ∪ {d, e, f, g}
∴ A∪B = {a, b, c, d, e, f, g}
Example #2
Suppose A = { x: x is an integer between 2 and 7} and B = { x: x is an integer between 5 and 10} then, find A∪B.
Here,
A = {3, 4, 5, 6}
B = {6, 7, 8, 9}
∴ A∪B = {3, 4, 5, 6, 7, 8, 9} = { x: x is an integer between 2 and 10}
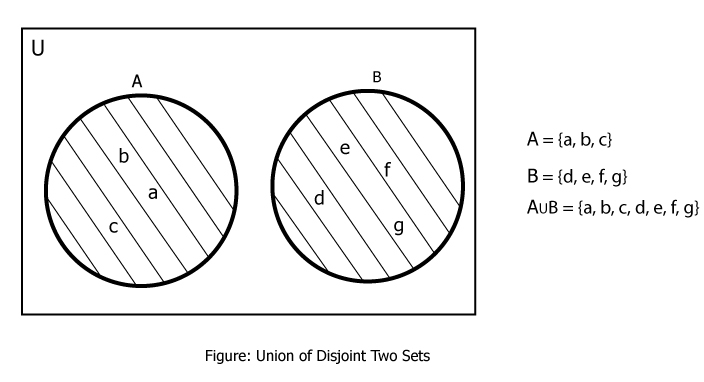
Example #3: Union of Disjoint Set With Venn Diagram
If A = {a, b, c} and B = {d, e, f, g}, find A∪B.
Here,
A∪B = {a, b, c} ∪ {d, e, f, g}
∴ A∪B = {a, b, c, d, e, f, g}
Example #4
Suppose A = { x: x is an odd integer} and B = { x: x is an even integer} then, find A∪B.
Here,
A = {..., -5, -3, -1, 1, 3, 5, ...}
B = {..., -4, -2, 0, 2, 4, 6, ...}
∴ A∪B = {..., -3, -2, -1, 0, 1, 2, ... } = {x: x is an integer}
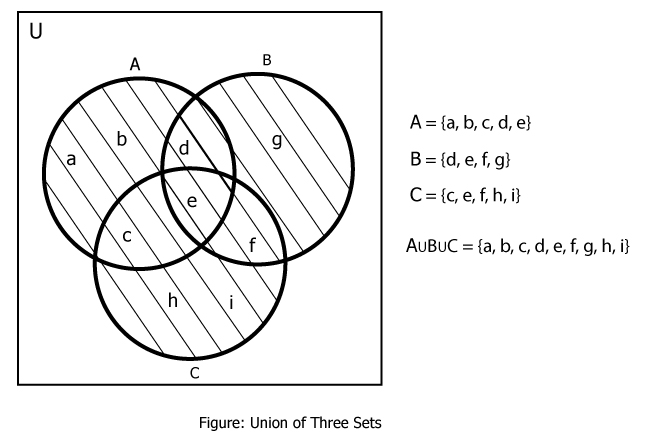
Example #5: Union of Three Sets With Venn Diagram
If A = {a, b, c, d, e}, B = {d, e, f, g} and C = {c, e, f, h, i}, find A∪B∪C.
Here,
A∪B∪C = {a, b, c, d, e} ∪ {d, e, f, g} ∪ {c, e, f, h, i}
∴ A∪B = {a, b, c, d, e, f, g, h, i}
Properties of Union of Set
Commutative Property
If A and B are two sets then, A∪B = B∪A
Suppose,
A = {1, 2, 3}
B = {3, 4, 5}
A∪B = {1, 2, 3, 4, 5}
B∪A = {3, 4, 5, 1, 2}
∴ A∪B = B∪A
Associative Property
If A, B and C are three sets then, A∪(B∪C)= (A∪B)∪C
Suppose,
A = {1, 2, 3}
B = {3, 4, 5}
C = {3, 1, 5, 8, 9}
B∪C = {3, 4, 5, 1, 8, 9}
A∪B = {1, 2, 3, 4, 5}
A∪(B∪C) = {1, 2, 3, 4, 5, 8,9}
(A∪B)∪C = {1, 2, 3, 4, 5, 8, 9}
∴ A∪(B∪C) = (A∪B)∪C
Identity Property
The union of a set and the empty set it that set itself, i.e, A∪ϕ = A.
Suppose,
A = {1, 2, 3}
B = ϕ = {}
A∪B = {1, 2, 3, } ∪ {} = {1, 2, ,3}
∴ A∪ϕ = A