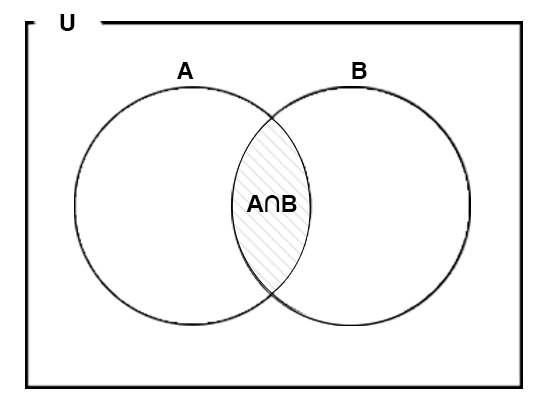
The intersection of two sets A and B ( denoted by A∩B ) is the set of all elements that is common to both A and B. In mathematical form,
For two sets A and B,
A∩B = { x: x∈A and x∈B }
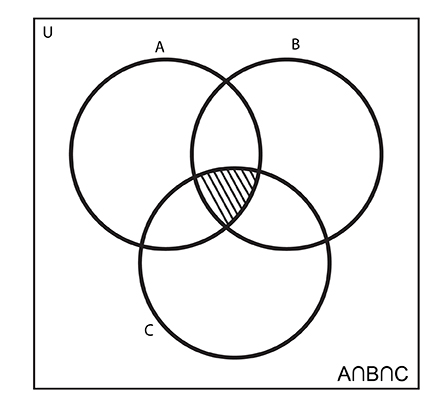
Similarly for three sets A, B and C,
A∩B∩C = { x: x∈A and x∈B and x∈C }
Intersection of Sets Examples
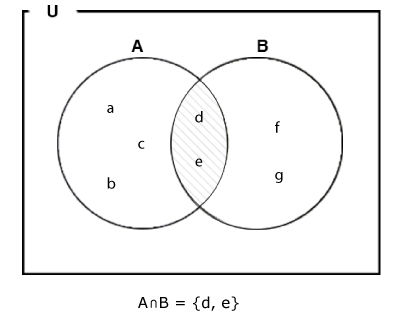
Example #1: Intersection of Two Sets With Venn Diagram
If A = {a, b, c, d, e} and B = {d, e, f, g}, find A∩B.
Here,
A = {a, b, c, d, e}
B = {d, e, f, g}
Now,
A∩B = {a, b, c, d, e} ∩ {d, e, f, g}
∴ A∩B = {d, e}
Example #2
Suppose A = { x: x is an integer between 1 and 7} and B = { x: x is an integer between 4 and 9} then, find A∩B.
Here,
A = {2, 3, 4, 5, 6}
B = {5, 6, 7, 8}
∴ A∩B = {5, 6} = { x: x is an integer between 4 and 7}
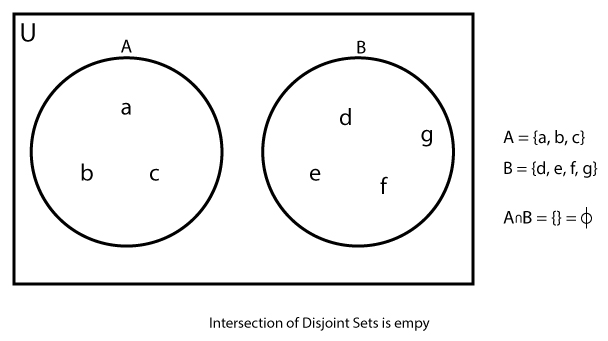
Example #3: Intersection of Disjoint Sets
If A = {a, b, c} and B = {d, e, f, g}, find A∩B.
Here,
A∪B = {a, b, c} ∩ {d, e, f, g}
∴ A∪B = {} = ϕ
Example #4
If A = { x: x is an integer} and B = { x: x is an even integer} then, find A∩B.
Here,
A = {..., -3, -2, -1, 0, 1, 2, ...}
B = {..., -2, 0, 2, ...}
∴ A∩B = {..., -4, -2, 0, 2, ... } = {x: x is an even integer}
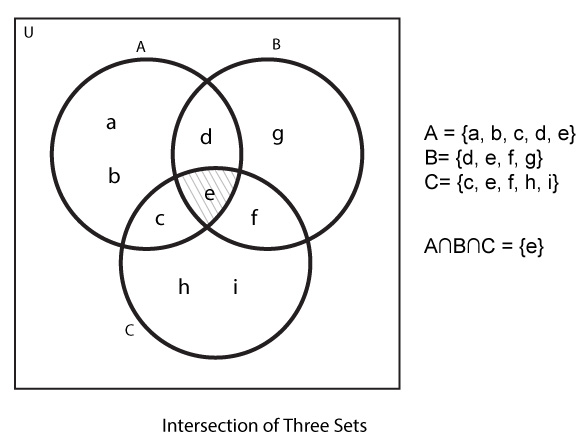
Example #5: Intersection of Three Sets With Venn Diagram
If A = {a, b, c, d, e}, B = {d, e, f, g} and C = {c, e, f, h, i}, find A∩B∩C.
Here,
A∩B∩C = {a, b, c, d, e} ∩ {d, e, f, g} ∩ {c, e, f, h, i}
The common element among all three sets is 'e'
∴ A∩B = {e}
Properties of Intersection of Sets
1. Commutative Property
If A and B are two sets then, A∩B = B∩A
Suppose,
A = {1, 2, 3, 4}
B = {4, 3, 5}
A∩B = {3, 4}
B∩A = {4, 3}
∴ A∩B = B∩A
2. Associative Property
If A, B and C are three sets then, A∩(B∩C)= (A∩B)∩C.
Suppose,
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
C = {3, 4, 1, 5, 8, 9}
B∩C = {3, 4, 5}
A∩B = {3, 4}
A∩(B∩C) = {3, 4}
(A∩B)∩C = {3, 4}
∴ A∩(B∩C) = (A∩B)∩C
3. Identity Property
The intersection of a set and the empty set is always the empty set, i.e, A∩ϕ = ϕ.
Suppose,
A = {a, b, c}
B = ϕ = { }
A∩B = {1, 2, 3, } ∩ {} = {} = ϕ
∴ A∪ϕ = ϕ