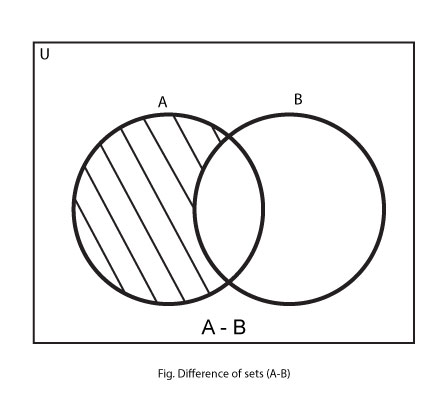
The difference of set B from set A, denoted by A-B, is the set of all the elements of set A that are not in set B. In mathematical term,
A-B = { x: x∈A and x∉B}
If (A∩B) is the intersection between two sets A and B then,
A-B = A - (A∩B)
Difference of Sets Example
Example #1
If A = { a, b, c, d, e } and B = { a, e, f, g}, find A-B and B-A.
The elements in only A are b, c, d and elements in only B are f, g. Thus,
A-B = {b, c, d}
and B-A = {f, g}
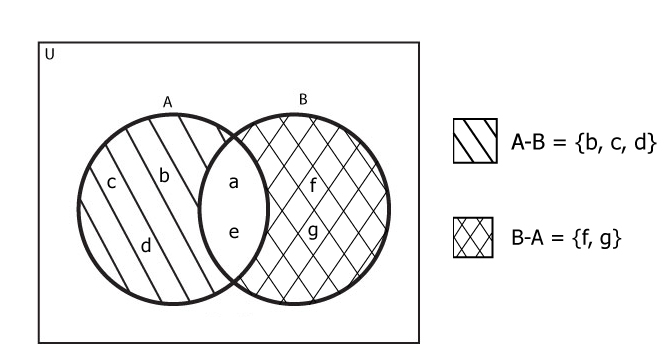
Notice that, A-B may not be equal to B-A.
Example #2
If A = { 1, 2, 4, 6, 8} and A-B = {1, 6, 8}, Find A∩B.
The intersection of A and B, (A∩B) is the set of all elements common in both A and B. Thus,
A∩B = A - (A-B)
or, A∩B = {2, 4}
Identities Involving Difference of Sets
- If set A and B are equal then, A-B = A-A = ϕ (empty set)
- When an empty set is subtracted from a set (suppose set A) then, the result is that set itself, i.e, A – ϕ = A.
- When a set is subtracted from an empty set then, the result is an empty set, i.e, ϕ – A = ϕ.
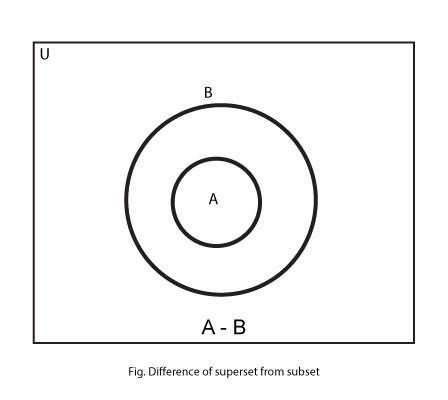
- When a superset is subtracted from a subset, then result is an empty set, i.e, A – B = ϕ if A ⊂ B
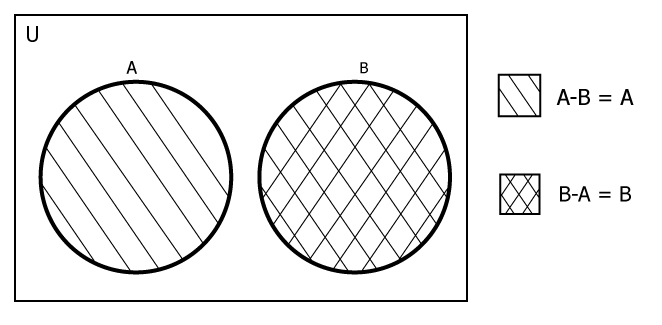
- If A and B are disjoint sets then, A-B = A and B-A = B