Cartesian Product - Mathstopia

For two sets A and B, the Cartesian product of A and B is denoted by A×B and defined as:

A×B = { (a,b) | aϵA and bϵB }

Cartesian Product is the multiplication of two sets to form the set of all ordered pairs. The first element of the ordered pair belong to first set and second pair belong the second set. For an example,

Suppose, A = {dog, cat}
         B = {meat, milk}  then, 
         A×B = {(dog,meat), (cat,milk), (dog,milk), (cat,meat)}

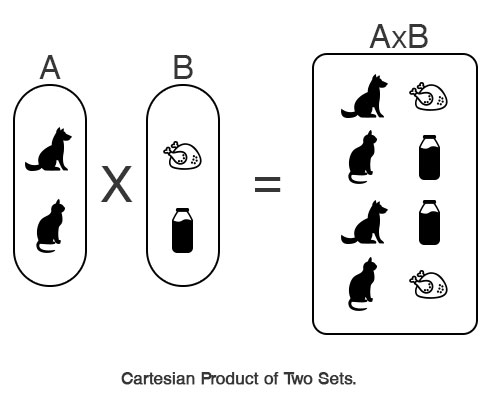
Cartesian product with visual example

Here, set A and B is multiplied to get Cartesian product A×B. The first element of A×B is a ordered pair (dog, meat) where dog belongs to set A. Similarly, second element of the ordered pair, meat belongs to set B. This is true for all elements(ordered pair) of A×B.

Cartesian Product Examples

Example #1: Practical Example on Cartesian Product

If X be the set of points on x-plane and Y be the set of points on y-plane then, X×Y represents the on XY plane.

Example #2

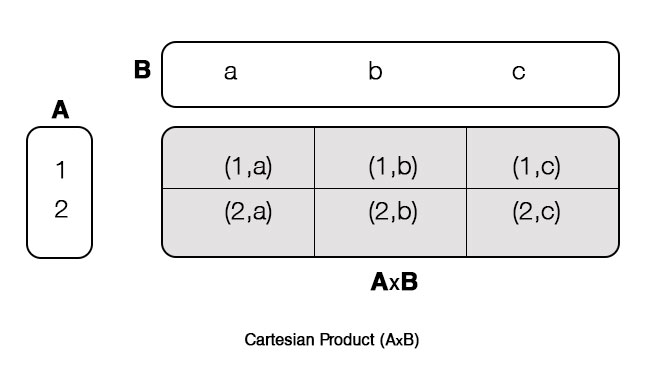
Suppose two sets A = {a, b} and B = {1, 2, 3}. Find A×B and B×A.

Here,
A = {a, b}
B = {1, 2, 3}
Now,
A×B = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}
B×A = {(1,a), (1,b), (2,a),(2,b), (3,a), (3,b)}

Cartesian product of two sets

Example #3

If A×B = { (x,1), (x,2), (x,3),(y,1), (y,2), (y,3)}. Find A and B.

Since, set A contains first element of each ordered pair only,

A = {x, y}

Since, set B contain second element of ordered pair only,

B = {1, 2, 3}

We exclude duplicate elements in both sets (because, set can only contain unique element).

Cartesian Product of 3 Sets

For three sets A, B and C, the Cartesian product of A, B and C is denoted by A×B×C and defined as:

A×B×C = { (p, q, r) | pϵA and qϵB and rϵC }

Example #4

Suppose two sets A = {-1, -2}, B = {1, 2} and C= {0}. Find A×B×C.

Here,
A = {-1, -2}
B = {1, 2}
C = {0}
Now,
A×B = {(-1,1,0), (-1,2,0), (-2,1,0), (-2,2,0)}

Key Points on Cartesian Product

Cartesian Product of Empty Set

If either of two set is empty, the Cartesian product of those two set is also an empty.

If A = {1, 2} and B = ϕ. Then, A×B = ϕ and B×A = ϕ.

Non-commutativity Property

For two unique and non-empty sets A and B, A×B is not equal to B×A.

If A = {a, b} and B = {1, 2, 3} then,

A×B = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}
B×A = {(1,a), (1,b), (2,a),(2,b), (3,a), (3,b)}

Here, A×B ≠ B×A

Condition for Commutative Property

For two sets A and B, the Cartesian product of two sets A×B and B×A are equal if either of the following condition is satisfied:

either of two set is empty
both sets are equal

If A = {1, 2} and B = ϕ. Then,

       A×B = ϕ
       B×A = ϕ
Hence, A×B = B×A

If A = B = {1, 2} then,

A×B = {(1,2), (2,2), (2,1), (2,2)}
B×A = {(1,2), (2,2), (2,1), (2,2)}
A×A = A² = {(1,2), (2,2), (2,1), (2,2)}
B×B = B² ={(1,2), (2,2), (2,1), (2,2)}

Hence, A×B = B×A = A² = B²