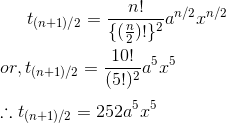Binomial Theorem and Expansion of Binomial Expression

The expression consisting of two terms is known as binomial expression. For example,

a+b
x+y

Binomial expression may be raised to certain powers. For example,

(x+y)2
(a+b)5

Expansion of Binomial Expression

In order to expand binomial expression, we use repeated multiplication. For example,

(a+b)2
= (a+b)(a+b)
= a(a+b) + b(a+b)
= a2 + 2ab + b2

(m+n)3
= (m+n)(m+n)2
= (m+n)(m2 + 2mn + n2)
= m(m2 + 2mn + n2) + n(m2 + 2mn + n2)
= m3 + 3m2n + 3mn2 + n3

Binomial Theorem

When power of expression increases, complexity of calculation of binomial expansion increases.To solve this problem, Isaac Newton introduced a theorem known as binomial Theorem.

Binomial Theorem Statement

For any positive integer n,

(a+x)n = C(n,0)an + C(n,1)an-1x + C(n,2)an-2x2 + ... + C(n,r)an-1xr+ ... + C(n,n)xn 

Proof of Binomial Theorem

Binomial theorem can be proved by using Mathematical Induction.

Principle of Mathematical Induction

Mathematical induction states that, if P(n) be a statement and if

1. P(n) is true for n=1,
2. P(n) is true for n=k+1 whenever P(n) is true for n=k.

then P(n) is true for all natural numbers n.

Now, let P(n) be the given statement. Then,

When n=1,
LHS = a+x
RHS = C(1,0)a+C(1,1)a1-1x = a+x
Hence, P(1) is true.

Let us assume that P(n) is true for some value n=k. Then,

(a+x)k = C(k,0)ak + C(k,1)ak-1x + C(k,2)ak-2x2 + ... + C(k,r)ak-1xr+ ... + C(k,k)xk 

Multiplying both sides by (a+x), we get

  (a+x)k+1 
= (a+x)[C(k,0)ak + C(k,1)ak-1x + C(k,2)ak-2x2 + ... + C(k,r)ak-1xr+ ... + C(k,k)xk]
= C(k,0)ak+1 + C(k,1)akx + C(k,2)ak-1x2 + ... + C(k,k)axk + C(k,0)akx + C(k,1)ak-1x2 + ... + C(k,k)xk+1 
= ak+1 + [c(k,1) + c(k,0)]akx + [c(k,2) + c(k,1)]ak-1x2 + [c(k,3) + c(k,2)]ak-2x3 + ... + xk+1
= C(k+1, 0)ak+1 + C(k+1, 1)akx + C(k+1, 2)ak-1x2 + ... + C(k+1, r)ak+1-rxr + C(k+1, k+1)xk 

Hence, P(k+1) is true whenever P(k) is true.

So, by principle of mathematical induction P(n) is true for all natural numbers n, i.e.

(a+x)n = C(n,0)an + C(n,1)an-1x + C(n,2)an-2x2 + ... + C(n,r)an-1xr+ ... + C(n,n)xn 

Similarly,

(a-x)n = C(n,0)an - C(n,1)an-1x + C(n,2)an-2x2 - . . . + (-1)rC(n,r)an-1xr+ ..... + (-1)nC(n,n)xn 

General Term in Binomial Expression

The general term in the expansion of (a+x)ⁿ is (r+1)^th term i.e.

tr+1 = C(n,r)an-rxr

Thus, First term(r=0), t1 = C(n,0)an
      Second term(r=1), t2 = C(n,1)an-1x1 and so on.

Now, the binomial theorem may be represented using general term as,

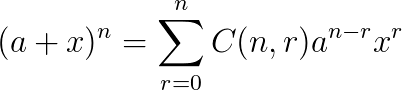
Middle term of Expansion

In order to find the middle term of the expansion of (a+x)ⁿ, we have to consider 2 cases.

1. When n is even: When n is even, suppose n = 2m where m = 1, 2, 3, …

Then, number of terms after expansion is 2m+1 which is odd. Thus, it has only one middle term which is (m+1)^th term. So,

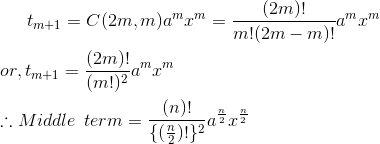
2. When n is odd: When n is odd, suppose n = 2m-1 where m = 1, 2, 3, …

Then, number of terms after expansion is 2m which is even. Thus, it has 2 middle terms which are m^th and (m+1)^th terms. So,

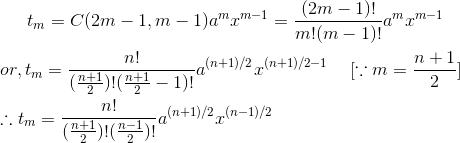
Binomial Expansion Examples

1. Expand (a+b)⁵ using binomial theorem.

Solution:

Here, the binomial expression is (a+b) and n=5.

So, using binomial theorem we have,

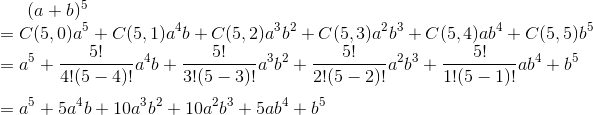
2. Find the middle term of the expansion (a+x)¹⁰.

Solution:

Since, n=10(even) so the expansion has n+1 = 11 terms. Hence there is only one middle term which is